2018-12-02

報告。`Dy`専用のSDFFontGeneratorツールを作りました。

報告

f:id:neuliliilli:20181201202946p:plain — ツールのウィンドウ画面

Dyゲームフレームワークのフォントレンダリングに必要するテクスチャをバッチで生成してくれるツールを作りましたことをご報告申し上げます。

2018-12-01

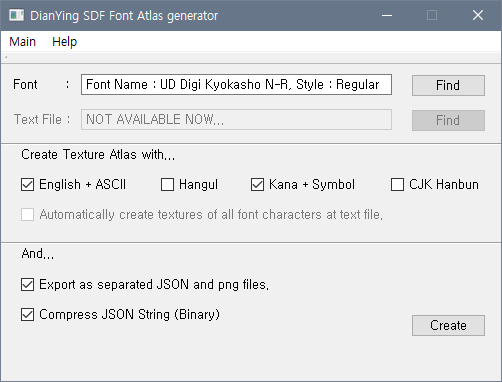
C++静的分析ツールのCppDependを使用してみた。

C++

CppDependとは

www.cppdepend.com

CppDependはCまたはC++のプロジェクトのコードを分析してコードの維持管理を容易くできるようにする分析ツールです。これを使うによって下記のことが把握できます。

コードの総量（LOC）が把握できる。
総コードとコメントとの割合が見れる。
プロジェクトに定義したタイプ、メソッドなどの数が確認できる。
レガシーコードの管理がしやすくなる。
プロジェクトのコード規則に違反したコードがあるかが確認できる。
技術的負債の比率が確認できる。
などなど…

実は以前に知り合いからから進められましたが、今更使うことになりました。今日使い始めましたし、お金もないから体験版をダウンロードしてしばらく使いたいと思います。

実はGitHubなどでオープンソース開発の目的で使用しているなら無料で使える方法があるようです。
プロジェクトに準じた文書とアクティビティを用意して、CppDependをサービスしている会社に送って無料で使わせたいと頼めば無料で使えるらしいです。ツールの定価はおよそ599ドルになりますし、個人の開発者はこのルートを通してツールを無料に使うようにするほうが良いと思います。

実際に使用して見ました。

f:id:neuliliilli:20181201180145p:plain — C++プロジェクト、`Dy`を静的分析した画像

最初分析をするのにおよそ10分くらい掛かりました。そしてこのように分析した結果の画面が見れます。このようにLOC、技術的負荷などが見れるようになります。

そしてこの画面でけじゃなくて、数値をクリックしてどの部分のどのコードが正しいかそれとも直すべきなのかをお知らせしてくれます。

例えば、右列のRules > Criticalをクリックしたらこのような画面が表示され、そして直すべきのコードを見せるようにしてくれます。

f:id:neuliliilli:20181201182215p:plain — イシューの個数、日で換算した技術的負荷の大きさなどが見れます。

そしてMetricsメニューではメソッドかタイプごとのLOCまたは複雑度を色で見せてくれます。全体の様相を把握したいならこれを見るほうが良いでしょうね。

f:id:neuliliilli:20181201182948p:plain — `Metrics`で見れるプロジェクトの全体的様相。

結論

技術的負荷を指すDebtは日々にどんどん増加するそうです。
規則違反、臭いコード（Code smell）、大きすぎるタイプなどが技術的負荷に当てはまります。ですから静的コード分析を行ってこのDebtを減らすようにリファクタリングなどをするほうが良いかもしれないですね。

2018-11-26

グラフ・最短距離アルゴリズムのまとめメモ（３）

Algorithm

序文

「グラフ・最短距離アルゴリズムのまとめメモ（２）」に引き続きJPS、~~JPS+、GoalBounding~~アルゴリズム（短距離アルゴリズム）を書きたいと思います。日本語下手ですので用語について指摘して頂けましたらありがとうございます。

本文

JPS（Jump Point Search）

http://users.cecs.anu.edu.au/~dharabor/data/papers/harabor-grastien-aaai11.pdf
Jump point search - Wikipedia
zerowidth.com

A. 論文分析（用語説明）

：あるノードから４方向または８方向への隣接ノードに移動する単位ベクトルを示す。
- もし ${\vec{d}}$ が斜め線である場合には、 ${\vec{d} = \vec{d_1} + \vec{d_2}}$ にもなれる。
${y = x + k\vec{d}}$ ：グラフのノード ${x}$ から ${y}$ まで直線の ${\vec{d}}$ 方向に ${k}$ 歩移動出来る。
${\pi = \left\langle n_0, n_1, ..., n_k \right\rangle}$ ：ノード ${n_0}$ から ${n_k}$ までの経路を表す。
${\pi \backslash x}$ ：経路 ${\pi}$ にノード ${x}$ は存在しない。
${p(x)}$ ：ノード ${x}$ の親ノードを表す。
${neighbours(x)}$ ：ノード ${x}$ から隣接したノード達を表す。
この論文では各ノードの４方向移動時の重みを ${1}$ 、そして斜め移動を $\sqrt{2}$ として規定している。
論文では８方向移動を前提とする。

B. Jump Pointsとは

f:id:neuliliilli:20181124165533p:plain

(a)では親 ${p(x)}$ から ${x}$ へ探索を続けているが、 ${x}$ の周りの灰色のノードを通して探索できることを表している。単純なA*ならば普通にノード ${x}$ に移動を終えて ${x.f(x)}$ を更新しているはずだが、JPSではそうしない。

代わりに、右へとずっと移動し続けて ${y}$ に到達するようにする。何故なら ${z}$ に移動をするつもりだからである。そして ${y.\pi = x}$ にする。（ ${p(x)}$ ではない）
${g(y)}$ を更新する。 ${g(y) = g(x) + \delta(x, y)}$ だ。
この過程を反復してもし障害物にぶつかったらこの方向への探索は終わる。（障害物とはたんなる障害物または重みが重い辺で繋がらノードを指す。）

Neighbour Pruning Rule

Pruning Ruleとは「枝刈りアルゴリズム」で、グラフまたはグラフのように今の状態から次への状態に移動できるイベント（枝）が指数的に急増する場合演算の量を減らしながら適切な解答を見つけるようにするアルゴリズムまたは規則を表す。
Neighbour Pruning Rule（NPR）では、目標に到達する為にノード ${x}$ の隣接ノードリスト ${neighbours(x)}$ の子ノード ${n}$ が計算されるかないかを判断する。
もし ${x}$ がスターティングポイントならNPRは適用しない。

f:id:neuliliilli:20181124175508p:plain

NPRは下の手順で進行する。

${(\pi = \left\langle p(x), ..., x, n \right\rangle)}$ と ${(\pi' \ \backslash \ x \ | \ \pi = \left\langle p(x), ..., n \right\rangle)}$ の重みの長さを比較する。
${\delta(p(x), x)}$ が（１）直線移動をするか（２）斜め移動をするかによってまた分かれる。
直線移動：次の数式を満たしている隣接したノード ${n}$ を枝刈りする。
${len({\left\langle} p(x), ..., n {\right\rangle} \ \backslash \ x) \le len(\left\langle p(x), x, n \right\rangle)}$
Fig. 2 (a)を見ると４番から ${x}$ へ移動した時、次となる ${n}$ は条件を満たしていない５番ノードになる。何故なら上の数式を適用した所、 ${2\sqrt{2} \le 2}$ になるからだ。
斜め移動：次の数式を満たしている隣接したノード ${n}$ を枝刈りする。
${len(\left\langle p(x), ..., n \right\rangle \ \backslash \ x) < len(\left\langle p(x), x, n \right\rangle)}$
Fig. 2 (c)を見ると８番から ${x}$ へ移動した時、次となる ${n}$ は条件を満たさない２，３，５番になる。
もし ${neighbours(x)}$ が障害物がなければ、灰色の隣接ノードは ${x}$ のNatural neighbourと呼ぶ。
定義１：Fig. 2 (b) Fig. 2(d)の様に障害物があって、障害物が無い場合には既存の数式を満たすにも関わらずに ${n}$ として選択されるノードをForced（強いられている）と言う。
- ${n}$ は以下の条件によって ${neighbours(x)}$ によって強いられる。(Forced) ${len(\left\langle p(x), x, n \right\rangle) < len(\left\langle p(x), ..., n \right\rangle \ \backslash \ x)}$
  よってFig. 2(b)では障害物がなければ５番ノードだけ選択するはずのものを３番が強いられて選択するようにした。
${len(\left\langle p(x), ..., n \right\rangle \ \backslash \ x)}$ を求めるのはさらなる部分的な最短経路問題になれる。

Arithmetic Description

定義２：でyがxのジャンプポイントとしたら、そのyは３つの条件で少なくとも１つ以上を満足する。
1. yはゴールだ。
2. yは ${neighbours(y)}$ のノードで少なくとも１つ以上が障害物によってForcedしたノードを持つ。
3. ${\vec{d}}$ は斜め移動である時、（１）か（２）の条件を満足するさらなる ${z = y + k_i\vec{d_i}}$ が存在する。

Fig 1. (b)は定義２を満足する図を見せる。 1. p(x)から出発する。p(x)スターティングポイントは【定義２：３】を満足する。何故なら次の子ノードとなるxが【定義２：２】満足するからだ。 * 真上のノードはxよりヒューリスティックじゃない為、廃棄する。 2. xから真上のノードか、真横のノードか、それともyに方向を展開する。しかし真上と真横は ${neighbours(x')}$ が無い為、排除する。そしてyが採択される。 3. 【定義２：１】を満足するためにzへと移動する。 4. 終わり。

このアルゴリズムは下のPseudo codeから確認できる。

// Identify successors
Required: x <= current node, s <= start position, g <= goal position
successors(x) = {};
n_neighbours(x) = prune(x, neighbours(x))
foreach n in n_neighbours(x) do
  n = jump(x, direction_unit(x, n), s, g)
  add n to successors(x)
return successors(x)

そしてJump関数は下のようになっている。

// Function `jump`
Required: x <= initial node, d: direction, s: start, g: goal
n := step(x, d)
if n is obstacle or oob then return null
if n == g then return n
if n' := neighbours(n) and n' is forced then return n
if d is diagonal then
  for all i := {1, 2} do
    if jump(n, d(i), s, g) is not null then return n
return jump(n, d, s, g)

実装

コード

長いです。

Relaxation

// @brief Relaxation function. 
// compare distance from start and push neighbor to minHeap.
void Relax(const DDirection& dir, SNode& cursor, SNode& successor, TMinHeap& heap, float distance) {
  if (successor.mDistantFromStart > cursor.mDistantFromStart + distance) {
    // Update distance from start and parent node in subgraph.
    successor.mDistantFromStart = cursor.mDistantFromStart + distance;
    successor.mParentPtr        = &cursor;

    // Set direction to parent node in predecessor subgraph.
    SetDirectionToParent(successor, dir);
    if (successor.status == ENodeStatus::Idle) { heap.push(&successor); }
    ++count;
  }
};

Prune (Neighbour Pruning Rule)

/// @brief  Find neighbour node list from cursor.
/// @param  cursor Point.
/// @return valid (natural and forced) neighbour node list from cursor.
[[nodiscard]] TNeighbourPairList Prune(SNode& cursor) 
{ 
  /// 0 1 /
  /// 3 x <-
  /// 6 7 /
  static auto DoPruneStraight = [](SNode& cursor, const int recCount) -> TNeighbourPairList {
    static constexpr std::array<std::pair<int, DDirection>, 5> checkList = {
        std::make_pair(0, gDirectionLU), std::make_pair(1, gDirection_U), 
        std::make_pair(3, gDirectionL_), std::make_pair(6, gDirectionLD), 
        std::make_pair(7, gDirection_D)
    };
    static constexpr std::array<std::pair<int, int>, 2> forcedCheckList = {
        std::make_pair(1, 0), std::make_pair(7, 6),
    };

    std::array<DDirection, 8> directionList = {};
    std::array<bool, 8>       obstacleFlag  = {};
    for (const auto& [id, dir] : checkList) {
      directionList[id] = GetRotatedDirectionCW(dir, recCount);
      if (cursor.GetEdge(directionList[id]).node == nullptr) { obstacleFlag[id] = true; }
    }

    TNeighbourPairList returnList = {};
    if (obstacleFlag[3] == false) { 
      returnList.emplace_back(directionList[3], cursor.GetEdge(directionList[3]).node);
    };

    for (const auto& [obs, flr] : forcedCheckList) {
      if (obstacleFlag[obs] == true && obstacleFlag[flr] == false) {
        returnList.emplace_back(directionList[flr], cursor.GetEdge(directionList[flr]).node);
      } 
    }

    return returnList;
  };
 
  /// 0 1 2
  /// 3 x 5
  /// 6 7 ↖
  static auto DoPruneDiagonal = [](SNode& cursor, const int recCount) -> TNeighbourPairList {
    static constexpr std::array<std::pair<int, DDirection>, 7> checkList = {
        std::make_pair(0, gDirectionLU), std::make_pair(1, gDirection_U), 
        std::make_pair(2, gDirectionRU), std::make_pair(3, gDirectionL_), 
        std::make_pair(5, gDirectionR_), std::make_pair(6, gDirectionLD),
        std::make_pair(7, gDirection_D)
    };
    static constexpr std::array<std::pair<int, int>, 2> forcedCheckList = {
        std::make_pair(5, 2), std::make_pair(7, 6),
    };

    std::array<DDirection, 8> directionList = {};
    std::array<bool, 8>       obstacleFlag  = {};
    for (const auto& [id, dir] : checkList) {
      directionList[id] = GetRotatedDirectionCW(dir, recCount);
      if (cursor.GetEdge(directionList[id]).node == nullptr) { obstacleFlag[id] = true; }
    }

    TNeighbourPairList returnList = {};
    static constexpr std::array<int, 3> generalCheckList = {0, 1, 3};
    for (const auto& id : generalCheckList) {
      if (obstacleFlag[id] == false) {
        returnList.emplace_back(directionList[id], cursor.GetEdge(directionList[id]).node);
      }
    }
    for (const auto& [obs, flr] : forcedCheckList) {
      if (obstacleFlag[obs] == true && obstacleFlag[flr] == false) {
        returnList.emplace_back(directionList[flr], cursor.GetEdge(directionList[flr]).node);
      } 
    }
    return returnList;
  };

  // Validity test
  assert(cursor.mParentPtr != nullptr);
  // Function body
  const DDirection& dirFromParent = GetReverseDirection(cursor.mParentDirection);
  if (IsDirectionDiagonal(dirFromParent) == true) 
  {
    const auto recursionCount = GetDirectionIndexFrom(gDirectionList4Diagonal, dirFromParent) * 2;
    assert(recursionCount != -2);
    return DoPruneDiagonal(cursor, recursionCount);
  }
  else
  {
    const auto recursionCount = GetDirectionIndexFrom(gDirectionList4, dirFromParent) * 2;
    assert(recursionCount != -2);
    return DoPruneStraight(cursor, recursionCount);
  }
};

Check Forced

/// @brief
/// @param  cursor
/// @param  direction
/// @return If there is any neighbour node which is forced, return true or false.
[[nodiscard]] bool IsForced(const SNode& cursor, const DDirection& direction) {
  /// 0 1 /
  /// 3 x <-
  /// 6 7 /
  static auto DoCheckStraight = [](const SNode& cursor, const int recCount) -> bool {
    static constexpr std::array<std::pair<int, DDirection>, 4> checkList = {
        std::make_pair(0, gDirectionLU), std::make_pair(1, gDirection_U), 
        std::make_pair(6, gDirectionLD), std::make_pair(7, gDirection_D)
    };
    static constexpr std::array<std::pair<int, int>, 2> forcedCheckList = {
        std::make_pair(1, 0), std::make_pair(7, 6),
    };

    std::array<DDirection, 8> directionList = {};
    std::array<bool, 8>       obstacleFlag  = {};
    for (const auto& [id, dir] : checkList) {
      directionList[id] = GetRotatedDirectionCW(dir, recCount);
      const auto& edge = cursor.GetEdge(directionList[id]);
      if (edge.node == nullptr) { obstacleFlag[id] = true; }
    }

    for (const auto& [obs, flr] : forcedCheckList) {
      if (obstacleFlag[obs] == true && obstacleFlag[flr] == false) { return true; } 
    }
    return false;
  };
 
  /// 0 1 2
  /// 3 x 5
  /// 6 7 ↖
  static auto DoCheckDiagonal = [](const SNode& cursor, const int recCount) -> bool {
    static constexpr std::array<std::pair<int, DDirection>, 4> checkList = {
        std::make_pair(2, gDirectionRU), std::make_pair(5, gDirectionR_), 
        std::make_pair(6, gDirectionLD), std::make_pair(7, gDirection_D)
    };
    static constexpr std::array<std::pair<int, int>, 2> forcedCheckList = {
        std::make_pair(5, 2), std::make_pair(7, 6),
    };

    std::array<DDirection, 8> directionList = {};
    std::array<bool, 8>       obstacleFlag  = {};
    for (const auto& [id, dir] : checkList) {
      directionList[id] = GetRotatedDirectionCW(dir, recCount);
      if (cursor.GetEdge(directionList[id]).node == nullptr) { obstacleFlag[id] = true; }
    }

    for (const auto& [obs, flr] : forcedCheckList) {
      if (obstacleFlag[obs] == true && obstacleFlag[flr] == false) { return true; } 
    }
    return false;
  };

  // Function body
  if (IsDirectionDiagonal(direction) == true) {
    const auto recursionCount = GetDirectionIndexFrom(gDirectionList4Diagonal, direction) * 2;
    assert(recursionCount >= 0);
    return DoCheckDiagonal(cursor, recursionCount);
  }
  else {
    const auto recursionCount = GetDirectionIndexFrom(gDirectionList4, direction) * 2;
    assert(recursionCount >= 0);
    return DoCheckStraight(cursor, recursionCount);
  }
}

Jump

[[nodiscard]] std::pair<SNode*, float> Jump(
    SNode& cursor, const DDirection& direction, 
    const SNode& goal, float distance = 0.0f) 
{
  SEdge& neighbourEdge = cursor.GetEdge(direction);
  const auto distanceToNeighbour = distance + neighbourEdge.mWeight;

  if (neighbourEdge.node == nullptr) { return {nullptr, 0}; }

  SNode& neighbourNode = *neighbourEdge.node;  

  if (neighbourNode.mPosition == goal.mPosition)  { return {&neighbourNode, distanceToNeighbour}; }
  if (IsForced(neighbourNode, direction) == true) { return {&neighbourNode, distanceToNeighbour}; }
  if (IsDirectionDiagonal(direction) == true) 
  {
    if (Jump(neighbourNode, direction.mH, goal, distanceToNeighbour).first != nullptr) 
    { return {&neighbourNode, distanceToNeighbour}; } 
    if (Jump(neighbourNode, direction.mV, goal, distanceToNeighbour).first != nullptr) 
    { return {&neighbourNode, distanceToNeighbour}; } 
  }
  return Jump(neighbourNode, direction, goal, distanceToNeighbour);
}

Get Successors

///
/// @brief  Get successors (next search nodes) from cursor.
/// @param  cursor
/// @return Valid node pointers list.
///
[[nodiscard]] TGetSuccessorsResult GetSuccessors(SNode& cursor, const SNode& goal) { 
  // Try prune or just get valid neighbours from cursor ( or start point ) 
  // If there is previous one (parent), do prune.
  TNeighbourPairList neighbourList = {};
  if (cursor.mParentPtr != nullptr) { neighbourList = Prune(cursor); }
  else { // Get neighbour from start point (s).
    for (const auto& direction : gDirectionList8) {
      const SEdge& edge = cursor.GetEdge(direction);
      if (edge.node == nullptr) { continue; }
      neighbourList.emplace_back(std::make_pair(direction, edge.node));
    }
  }

  // Try jump to all valid neighbour nodes and get successors for these.
  TGetSuccessorsResult returnList = {};
  for (const auto& [direction, neighbour] : neighbourList) {
    auto [successorNode, distance] = Jump(cursor, direction, goal, 0);
    if (successorNode == nullptr) { continue; }

    successorNode->mParentPtr = &cursor;
    SetDirectionToParent(*successorNode, direction);
    returnList.emplace_back(direction, distance, successorNode);
  }
  return returnList;
}

Main

void JPS(TMazeContainer& map, const DVector2& start, const DVector2& goalPos) {
  // Update huristic functions.
  for (auto& row : map) {
    for (auto& node : row) {
      if (node.type == ENodeType::Floor) { node.UpdateHuristicValueToGoal(goalPos); }
    }
  }

  // Start point setting.
  auto& startNode = map[start.y][start.x]; 
  startNode.mDistantFromStart = 0.0f;      
  TMinHeap minHeap{MinHeapCmp};       
  minHeap.push(&startNode);

  // Do JPS
  while (minHeap.empty() == false) {  
    SNode& cursor = *minHeap.top(); minHeap.pop();    // Extract-Min
    cursor.status = decltype(SNode::status)::Visited; // Move into `S` set.
    if (cursor.mPosition == goalPos) { return; }      // Check goal point.

    auto successors = GetSuccessors(cursor, map[goalPos.y][goalPos.x]);
    for (auto& successorInstnace : successors) {
      const auto& direction = successorInstnace.mDirection;
      const auto  distance  = successorInstnace.mDistance;
      auto&       successor = *successorInstnace.mSuccessor;
      Relax(direction, cursor, successor, minHeap, distance);
    }
  }
}

結論

f:id:neuliliilli:20181126002802p:plain

既存のA*よりすごく速くなりました。理論上２倍から４倍くらいの速さを見せるそうです。ですが、ここで前処理を行って実行するJPS+を使うとA*よりなんと60倍くらい速くなるそうです。

しかしまた分量調整大失敗で、JPS+とGoalBoundingは（４）に分けて書きたいと思います。すみません。。。うげー

2018-11-24

グラフ・最短距離アルゴリズムのまとめメモ（２）

Algorithm

序文

「グラフ・最短距離アルゴリズムのまとめメモ（１）」に引き続き、Dijkstra、Bellman-ford、A*、そしてJPSから派生した最短距離アルゴリズムを書きたいと思います。日本語下手ですのでちょっと用語について指摘して頂けましたらありがとうございます。

参照

INTRODUCTIONS TO ALGORITHMS 3rd EDITION Chapter 22
INTRODUCTIONS TO ALGORITHMS 3rd EDITION Chapter 24
ダイクストラ法 - Wikipedia
ベルマン–フォード法 - Wikipedia
A* 보다 빠른 JPS 알고리즘 : 네이버 블로그

本文

0. 本格的に入る前に知っておきたかったもの。

Introduction to algorithm 3edのChapter24初頭から新たに知ったものと確実ししたのをメモしました。

最短経路問題では重みがある辺があるグラフ、 ${G = (V, E)}$ と各辺に実数の重みを計算する関数 ${w : E \rightarrow \mathbf{R}}$ が与えられる。（本では「方向がある辺」と書いているが、非負数の重みがある以上元のノードには戻らない。）そして任意の経路 ${p = \left\langle v_0, v_1, ..., v_k \right\rangle}$ の重みはその経路を構える辺の重みを乗算したものと一致する。

即ち ${w(p) = \sum_{i=1}^{k} w(v{i-1}, v{i})}$ である。

BFSは重みが全部1のグラフで最短経路を探すアルゴリズムである。
最短経路問題を解くアルゴリズムは普通２つのノードの間の最短経路がその中にある部分最短経路を含めるという特性を利用する。これを「最短経路の部分構造最適性」という。
最短経路の部分構造最適性があるということは、動的計画法（DP）または貪欲法（どんよくほう、Greedy Algorithm）が適用出来る可能性あるということを指す。
そして今からまとめる「ダイクストラ法」「ベルマン・フォード法」この記事ではないが「ワーシャル–フロイド法」はそれぞれ貪欲法、動的計画法を使用している。

整理24.1：最短経路の全ての部分最短経路は最短経路である。

もしグラフの中である辺の重みが負数であるかもしれない。あるとしても負数の辺によって最短経路を求める為循環（サイクル）しなければ影響はない。しかし負数の重みによって無限に循環するようになったらスターティングポイントの ${s}$ から到着点 ${v}$ までの最短経路は取れない。そしてsからvまでの重みは ${\delta(s, v) = -\infty}$ と定義できる。
最短経路は負数の辺を持つ循環経路にはならない。そして非負数の重みを持つ循環も含められない。
重みが0がある辺がある循環を持つ最短経路がある場合には、その循環を含まずにもできる最短経路が存在する。

最短経路の表現

最短経路問題を解く途中で構成されるPrecessor Subgraph ${G_{\pi} = (V\pi, E\pi)}$ に対し、 ${v.\pi}$ の値は最短経路の親ノードを指していないかもしれない。
ただし、最短経路問題のアルゴリズムで結果的に出す ${G_{\pi} = (V\pi, E\pi)}$ 部分グラフでは全ての ${v.\pi}$ は最短経路を構成するための親ノードを指していることがわかる。

緩和（Relaxation）

最短経路問題のアルゴリズムはRelaxationを使う。グラフの全てのノートvの距離 ${v.d}$ は最初に ${\infty}$ に初期化される。その過程に ${\Theta(V)}$ 時間が掛かる。
Relaxationの途中に最短経路の推定値である ${v.d}$ を減らし、そして ${v.\pi}$ を更新することも出来る。Relaxationが発動する条件は、今の距離dが辺の重みと親となるノードのd距離と乗算した値を超えていたら緩和が発動する。

1. ダイクストラ法（Dijkstra）

グラフ（方向を持つ辺があるグラフでも良い） ${G = (V, E)}$ にて全ての辺の重みが非負数ではない場合に最短経路を探せる。
効率的に実装すれば２．ベルマン・フォード法より速度は速い。
貪欲法を使う。

More deep inside

ダイクストラ法はスターティングポイント ${s}$ からの最短経路の重みの合が最終的に決められたノードの集合 ${S}$ を管理する。
現在最短経路の重みの合最も少ないノードから辺として繋がる隣接したノード ${u \in V - S}$ に対し緩和を行う。それを反復的に実行する。
重みの合が一番少ない、まだ ${S}$ に入っていないノードを探すには二分ヒープ（最小ヒープ）を使用する。
そして全てのノードが ${S}$ にあったらアルゴリズムは実行を終える。
while各ルーフの最初の時点で全てのノード ${v \in S}$ に対し ${v.d = \delta(s, v)}$ である。
ダイクストラ法の時間複雑度は、Queueをどう実装するかによって３つに分かれる。
1. 全てのノードを一列にリストに入れてQueueを維持すること。INSERTとDECREASE-KEYは ${O(1)}$ になるが、ルーフごとに重みが一番少ないノード（Sに入っていない）を選ばなきゃならないためEXTRACT-MINは ${O(V)}$ になる。そして最悪 ${O(V^{2} + E)}$ の時間複雑度を見せられる。
2. グラフの密度が低ければ二分ヒープの最小ヒープを使用して向上させられる。この場合にはINSERT DECREASE-KEY EXTRACT-MIN全部 ${O(V)}$ になる。したがって時間複雑度は ${O((V + E)\lg{V})}$ になる。
3. 一番難しい方法だが、フィボナッチヒープを使用して時間複雑度 ${O(V\lg{V} + E)}$ が得られる。

コード

実装したコードは時間複雑度が ${O((V + E)\lg{V})}$ を見せる２番目の方法だ。

// @brief Compare function of minHeap.
// if true, left is previous to right in heap container.
static auto MinHeapCmp = [](const SNode* left, const SNode* right) { 
  return left->dist_from_start < right->dist_from_start; 
}; 
using THType = SNode*;
using TMinHeap = std::priority_queue<THType, std::vector<THType>, decltype(MinHeapCmp)>;

// @brief Relaxation function. 
// compare distance from start and push neighbor to minHeap.
static auto Relax = [](const EDirection dir, const THType cursor, THType neighbor, 
                       TMinHeap& heap) {
  assert(neighbor != nullptr && cursor != nullptr);
  if (neighbor->dist_from_start > cursor->dist_from_start + 1) {
    // Update distance from start and parent node in subgraph.
    neighbor->dist_from_start = cursor->dist_from_start + 1;
    neighbor->parent          = cursor;
    // Set direction to parent node in predecessor subgraph.
    SetDirectionToParent(*neighbor, dir);
    if (neighbor->status == ENodeStatus::Idle) { heap.push(neighbor); }
  }
};

void Dijkstra(TMazeContainer& map) {
  map[0][0].dist_from_start = 0;      // (0) Initialize starting point.
  TMinHeap minHeap{MinHeapCmp};       // (1) Insert start node to min_heap
  minHeap.push(&map[0][0]);

  while (minHeap.empty() == false) {  // (2) Do dijkstra comparing distances.
    THType cursor   = minHeap.top(); minHeap.pop();     // Extract-Min
    cursor->status  = decltype(SNode::status)::Visited; // Move into `S` set.

    for (auto dir = 0; dir < 4; ++dir) {                // Relaxation procedure
      auto& neighbor = cursor->neighbors[dir];
      if (neighbor.node == nullptr) { continue; }
      Relax(static_cast<EDirection>(dir), cursor, neighbor.node, minHeap);
    }
  }
}

2. ベルマン–フォード法（Bellman-ford）

負数の重みがある時にも使われる。
負数の重みがある循環経路があるときには皮膚数を持つ循環経路があるかを返すようにする。
- 重みが皮膚数の循環があるならグラフでの最短経路 ${\delta(s, v)}$ は存在しない。

More deep inside

ダイクストラ法とは違って理論上「状態」を持たない。しかし、コードでは皮膚数による循環を防ぐために状態を持つようにする。
BFSとの違いはBFSは重みが無いか単位の重みである反面、ベルマン・フォード法は辺のそれぞれの重みがある。
時間複雑度は ${O(VE)}$ である。何故なら全てのノード ${|V| - 1}$ で全ての辺 ${\Theta(E)}$ を調査するからだ。

コード

コードでは簡単なQueueを使ってノードの順番を指定する。

using THType = SNode*;
using TQueue = std::queue<THType>;
// @brief Relaxation function. 
// compare distance from start and push neighbor to minHeap.
static auto Relax = [](const EDirection dir, const THType cursor, THType neighbor, TQueue& queue) {
  assert(neighbor != nullptr && cursor != nullptr);
  if (neighbor->dist_from_start > cursor->dist_from_start + 1) {
    // Update distance from start and parent node in subgraph.
    neighbor->dist_from_start = cursor->dist_from_start + 1;
    neighbor->parent          = cursor;
    // Set direction to parent node in predecessor subgraph.
    SetDirectionToParent(*neighbor, dir);
    if (neighbor->status == ENodeStatus::Idle) { queue.emplace(neighbor); }
  }
};

// @brief Validation process whether or not there is negative cycle.
static auto DoValidation = [](const THType cursor, const THType neighbor) {
  assert(neighbor != nullptr && cursor != nullptr);
  if (neighbor->dist_from_start > cursor->dist_from_start + 1) {
    return false;
  }
  return true;
};

// @brief Do bellman-ford algorithm.
[[nodiscard]] bool BellmanFord(TMazeContainer& map) {
  // Initialize starting point.
  map[0][0].dist_from_start = 0; 
  TQueue nodeQueue {}; nodeQueue.emplace(&map[0][0]);

  // Do bellman-ford algorithm.
  while (nodeQueue.empty() == false) { 
    auto& node = *nodeQueue.front(); nodeQueue.pop();
    node.status = ENodeStatus::Visited;

    // Relaxation procedure
    for (auto dir = 0; dir < 4; ++dir) { 
      auto& neighbor = node.neighbors[dir];
      if (neighbor.node == nullptr) { continue; }
      Relax(static_cast<EDirection>(dir), &node, neighbor.node, nodeQueue);
    }
  }

  // Do validation of negative weight cycle.
  for (auto& row : map) { 
    for (auto& node : row) {
      if (node.type != ENodeType::Floor) { continue; }
      for (auto dir = 0; dir < 4; ++dir) {                
        auto& neighbor = node.neighbors[dir];
        if (neighbor.node == nullptr) { continue; }
        if (DoValidation(&node, neighbor.node) == false) { return false; };
      }
    }
  }
  return true;
}

3. A*（A-Star）

A* search algorithm - Wikipedia

正確度と性能が高く、実際にゲームエンジンなどでよく使われるアルゴリズム。そしてダイクストラ法かベルマン・フォード法みたいな基本的なアルゴリズムを除き一番広まっているアルゴリズムでもある。
ダイクストラ法の拡張版。しかしダイクストラ法は貪欲法を使って目の前（ノードから隣接したノード）へのノードの間の距離を最短として最短経路を探す反面、A-starはヒューリスティックを使用して貪欲法とはちょっと違う様相を見せる。
A*アルゴリズムはグラフ全体の情報が得られないと最短経路が解けない。（Informed search algorithm）
ダイクストラ法より遥かに速い。

More deep inside

A*は各ループでスターティングポイント ${s}$ からゴール ${v}$ までの距離を推定して進行する道を選ぶ。

これを数式を表現んすると

${f(n) = g(n) + h(n)}$

になる。

${g(n)}$ はスターティングポイント ${s}$ から現在のノード ${n}$ までの距離（多分 ${\delta(s, n)}$ じゃないかなと）である。
${h(n)}$ はヒューリスティック関数で、今のノード ${n}$ からゴール ${v}$ までに推定した最短距離の重み（コスト）を関数げ表現したものだ。
`A*の終了条件は２つか一つ以上を満たす。
1. ${s}$ から ${v}$ まで繋がった場合
2. グラフで進行する辺がもう残されていない場合
の推定数値がただしければA*により求める最短距離は最短距離であることを保障する。
- 普通は最短距離ではなく、それに準ずる短距離が取れる。

実装

A*を実装するにはダイクストラ法のように二分ヒープを使う。（多分フィボナッチヒープも出来るはず？）
二分ヒープに入るものは ${f(n)}$ か、それとも ${f(n)}$ を持っているノードへの参照になる。
各ループごとに一番が低いノードを取り出して隣接するノードのとを更新する。そいて隣接ノードが最小ヒープに入る。
- ${n'.h(n)}$ の値は固定である。ヒューリスティック関数は簡単にはゴールまでの直線距離として実装する。
最小ヒープが空っぽか、それとも ${v.f(n)}$ が一番低い時に終了する。その時 ${v.h(n) = 0}$ になる。

コード

// @brief Compare function of minHeap. 
// if true, left is previous to right in heap container.
static auto MinHeapCmp = [](const SNode* left, const SNode* right) { 
  return left->GetF() < right->GetF();
};

using THType = SNode*;
using TMinHeap = std::priority_queue<THType, std::vector<THType>, decltype(MinHeapCmp)>;

// @brief Relaxation function. 
// compare distance from start and push neighbor to minHeap.
static auto Relax = [](const EDirection dir, const THType cursor, THType neighbor, 
                       TMinHeap& heap) {
  assert(neighbor != nullptr && cursor != nullptr);
  if (neighbor->dist_from_start > cursor->dist_from_start + 1) {
    // Update distance from start and parent node in subgraph.
    neighbor->dist_from_start = cursor->dist_from_start + 1;
    neighbor->parent          = cursor;
    // Set direction to parent node in predecessor subgraph.
    SetDirectionToParent(*neighbor, dir);
    if (neighbor->status == ENodeStatus::Idle) { heap.push(neighbor); }
  }
};

// @brief Do Astar algorithm to [0, 0] -> [goalX, goalY].
// If [goalX, goalY] disappear in priority_queue (moved into S), halt algorithm
// and show result.
void Astar(TMazeContainer& map, const DVector2& start, const DVector2& goalPos) {
  auto& startNode = map[start.x][start.y];
  startNode.dist_from_start = 0;      
  TMinHeap minHeap{MinHeapCmp};       
  minHeap.push(&startNode);

  while (minHeap.empty() == false) {  
    THType cursor   = minHeap.top(); minHeap.pop();     // Extract-Min
    if (cursor->mPos == goalPos) { return; }            // Check goal point.
    cursor->status  = decltype(SNode::status)::Visited; // Move into `S` set.
    for (auto dir = 0; dir < 4; ++dir) {                // Relaxation procedure
      auto& neighbor = cursor->neighbors[dir];
      if (neighbor.node == nullptr) { continue; }
      Relax(static_cast<EDirection>(dir), cursor, neighbor.node, minHeap);
    }
  }
}

結論

分量調整ダイ失敗しました。（３）に分けて書きます。うげー

2018-11-23

グラフ・最短距離アルゴリズムのまとめメモ（１）

Algorithm

序文

自分の頭の中で纏まらなくてブログで復習を兼ねて書きたいと思います。そしていろいろと調べたりして基本以外にもある良いアルゴリズムも纏めて書こうしました。

参照

INTRODUCTIONS TO ALGORITHMS 3rd EDITION Chapter 22

幅優先探索 - Wikipedia

深さ優先探索 - Wikipedia

本文

1. BFS（幅優先探索）

一番単純な探索アルゴリズム。しかしDijkstra、Primの元となるアルゴリズムである。
${G= (V, E)}$ グラフとスターティングポイント（Source） ${s}$ を根ノードとし到達できる全ての任意位置を探して距離を計算する。
${s}$ からの距離が ${k+1}$ であるノードを探索する前に、 ${k}$ のノードを全て探索する。BFSという名はグラフでの探索した領域を広めるということで名付けられた。
BFS自体はヒューリスティックを使っていないため、グラフ全体を目的のノードがみつかるまで、目的のノードに接近しているかどうかなどは考慮せず探索する。
BFSはDirected、Indirected全てのグラフに適用できる。
BFSによって生成されたツリーの形は一つに限られている。
BFSは最適である。

More deep inside

BFSを実装するときに、各ノードに対して状態は3つを持つ。
1. 白：まだ探索されていない場合。
2. グレー：白から変わり、後の探索の為にQueueに入っている場合。
3. 黒：探索済み。BFSは全てのノードが一度しか発見されない。
各ノードに対して一度しか発見されないため、各ノードの親ノードは最大一個まで持つ。
ノードの状態が【黒】なら隣接する全てのノードは【白】ではない。
Queueに入っているノードの状態はいつも【グレー】である。
BFSの時間複雑度は ${O(V + E)}$ だ。何故なら ${O(V)}$ はグラフの全てのノードをQueueに入れることによって、そして ${O(E)}$ は任意ノードにて隣接するノードを探索する時に繋がる辺の総合が ${\Theta(E)}$ だからだ。

コード

void BFS(TMazeContainer &map) {
  auto &start = map[0][0];  start.dist_from_start = 0;
  std::queue<SNode*> queue; queue.push(&start);

  while (!queue.empty()) {
    auto present = queue.front();

    for (auto dir = 0; dir < 4; ++dir) {
      auto &neighbor = present->neighbors[dir];
      if (neighbor.node == nullptr) { continue; }
      if (neighbor.node->status == ENodeStatus::Stay) { continue; }

      auto next = neighbor.node;
      if (next->status == ENodeStatus::Idle) {
        next->status = ENodeStatus::Stay;
        next->dist_from_start = present->dist_from_start + 1;
        next->parent = present;

        switch (static_cast<EDirection>(dir))
        {
        default: break;
        case EDirection::Up:    next->parent_dir = EDirection::Down;  break;
        case EDirection::Down:  next->parent_dir = EDirection::Up;    break;
        case EDirection::Left:  next->parent_dir = EDirection::Right; break;
        case EDirection::Right: next->parent_dir = EDirection::Left;  break;
        }

        queue.push(next);
      }
    }

    present->status = ENodeStatus::Visited;
    queue.pop();
  }
}

2. DFS（深さ優先探索）

BFSとは違ってDFSはノードから可能な限り深く検索することを目指している。
グラフ ${G= (V, E)}$ から一番最近に発見して、まだ調査されていない辺を持つノード ${v}$ からスタックや再帰を活用して最後まで探索する。
${v}$ から派生した全ての辺が調査したら、ノード ${v}$ を発見してくれたノードに隣接する他のノードを調査するためにスタックを巻き戻す。
BFSとは違って、スターティングポイントが複数存在しうる。何故ならDFSは最短距離を測るためのアルゴリズムとして使用するのではなく一般的には別のアルゴリズムのサブルーチンとして活用するからだ。（BFSは上記でもあるように最短距離によく使われる）
DFSは最適ではない。完全でもない。
DFSはトポロジカルソートに使用される。

More deep inside

DFSを実装するときに、各ノードに対して状態は3つを持つ。
1. 白：まだ探索されていない場合。
2. グレー：辺のよって発見されてStackに入っていてから、ついに探索の対象となったとき変わる。
3. 黒：隣接した辺による再帰が終わってから探索済みになる時、変わる。
各ノードに対して一度しか探索対象とされないため、各ノードの親ノードは最大一個まで持つ。
そしてDFSは残されたノードに対して任意位置のノード（白）からまたDFSを行えるので親へのグラフが一つより多くなる場合もある。なのでDFSで構築された深さ優先ツリーはフォレスト（Forest）を形成する。（predecessor subgraph）
DFSの時間複雑度は ${\Theta(V + E)}$ だ。

タイムスタンプ

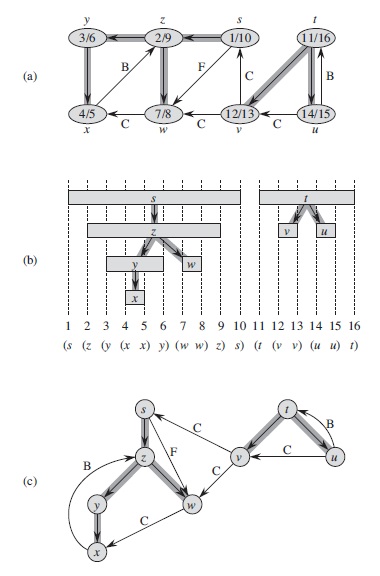Introduction To Algorithm 3ed p620 fig 22.5

DFSは探索する時に時間を記録する。そして各ノード ${v}$ は2つの時間記録を持つ。一つ目 ${v.d}$ は ${v}$ ノードが最初に探索対象となった時に、二つ目は対象となるノードに隣接する辺による再帰探索が終わった後に記す。これによってグラフの構造に重要な情報をもたらすらしい。

コード

auto sTime = 0u;

void DFS_Internal(TMazeContainer& map, SNode& cursor);
void DFS(TMazeContainer& map) {
  sTime = 0u;
  for (auto& xList : map) { // Y
    for (auto& element : xList) { // X
      // FIND ANY WHITE NODE
      if (element.status == ENodeStatus::Idle) { 
        element.dist_from_start = 0;
        DFS_Internal(map, element);
      }
    }
  }
}

void DFS_Internal(TMazeContainer& map, SNode& cursor) {
  cursor.status = ENodeStatus::Stay;
  sTime += 1; cursor.timestamp.startSearch = sTime;

  for (auto dir = 0; dir < 4; ++dir) {
    auto &neighbor = cursor.neighbors[dir];
    if (neighbor.node == nullptr)                   { continue; }
    if (neighbor.node->status != ENodeStatus::Idle) { continue; }

    auto *next = neighbor.node;
    next->dist_from_start = cursor.dist_from_start + 1;
    next->parent = &cursor;
    neighbor.is_traversed = true;

    switch (static_cast<EDirection>(dir)) {
    default: break;
    case EDirection::Up:    next->parent_dir = EDirection::Down;  break;
    case EDirection::Down:  next->parent_dir = EDirection::Up;    break;
    case EDirection::Left:  next->parent_dir = EDirection::Right; break;
    case EDirection::Right: next->parent_dir = EDirection::Left;  break;
    }
    DFS_Internal(map, *next);
  }
  sTime += 1; cursor.timestamp.endSearch = sTime;
}

結論

一つでまとめようとしましたけど出来ませんでした。
肝心のDijkstra、Bellman-ford、A*、そしてもっと高級のアルゴリズムは（２）にて書きます。